1.1.3 Energía Interna y Entalpía

Energía Interna

La magnitud que designa la energía almacenada por un sistema de partículas se denomina energía interna (U). La energía interna es el resultado de la contribución de la energía cinética de las moléculas o átomos que lo constituyen, de sus energías de rotación, traslación y vibración, además de la energía potencial intermolecular debida a las fuerzas de tipo gravitatorio, electromagnético y nuclear.
La energía interna es una función de estado, es decir, sólo depende del estado inicial y del estado final.

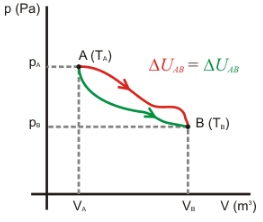
Como consecuencia de ello, la variación de energía interna en un ciclo es siempre nula, ya que el estado inicial y el final coinciden:


 El calor intercambiado en un proceso viene dado por:



Siendo C la capacidad calorífica. En este proceso, por realizarse a volumen constante, se usará el valor Cv (capacidad calorífica a volumen constante). Entonces, se obtiene finalmente:



ENTALPÍA


La entalpía es una propiedad creada que agrupa todas las formas de energía disponibles en una sustancia que fluye. En su forma más simple la entalpía se define como la suma de la energía interna y la energía de flujo así:

∆H = U + p∆V

Dónde:
• H es la entalpía (en Joules).
• U es la energía interna (en Joules).
• p es la presión del sistema (en Pascales).
• V es el volumen del sistema (en metros cúbicos).
La energía transferida en forma de calor por un sistema durante un proceso que ocurre a presión constante es igual al cambio en la entalpía del sistema.

La entalpía es una propiedad de estado de un sistema, con lo cual se puede decir que el sistema tiene un determinado valor de entalpía. Cuando el sistema cambia de un estado inicial a un estado final, cambian las propiedades de estado.

El cambio en la entalpía, como es una propiedad de estado, depende tan sólo de las condiciones iniciales y finales, es decir, es la diferencia entre la cantidad inicial y la final,

∆H = Hfinal - Hinicial

En una reacción, se puede escribir el cambio en la entalpía como
∆H = Hproductos - Hreactivos

Las características de la entalpía:
a.                  Es una propiedad extensiva, es decir, es directamente proporcional a la cantidad de reactivo consumido en el proceso.
b.                  El cambio de entalpía para una reacción tiene la misma magnitud pero signo opuesto para la reacción inversa.
c.                  El cambio de entalpía para una reacción depende del estado de agregación de los reactivos  y de los productos.

Ejemplo de muestra

1.       
La hidracina reacciona con el cloro de acuerdo a la siguiente reacción:

N2H4 (l) Cl2 (g) → 4HCl (g) N2 (g)

∆H= 420 kJ

a)      Calcular el cambio en la entalpía cuando 10 g de hidracina reaccionan con un exceso de cloro.
b)      Calcular el cambio en la entalpía cuando se generan 1.5 moles de HCl(g)

Para resolver el primer inciso, primero se calcula la cantidad de moles que hay en 10 g de hidracina. La masa molar de la hidracina es 32 g/mol. Con lo cual:

10 g de hidracina = 1 mol de hidracina 32g de hidracina = 0.31 moles de hidracina

Con saber que el cambio en la entalpía de 420 kJ corresponde a un mol de hidracina, se puede calcular el cambio de entalpía asociado con 0.31 moles como se observa

H = 0.31 moles de hidracina -420 kj 1  mol de hidracina = -130.2 kJ

Para resolver el segundo inciso es necesario utilizar los coeficientes estequiométricos. El cambio en la entalpía es 420 kJ cuando se producen 4 moles de HCl (coeficiente estequiométrico igual a 4). Ahora se generan 1.5 moles, con lo cual el cambio en la entalpía es
H = 1.5 moles de HCI -420 kj4 moles HCl = -157.5 kJ

Observa que en los 2 casos el valor de H es negativo, porque la dirección de la reacción no se ha visto modificada. En todos los casos, las reacciones son exotérmicas.









El cambio estándar de entalpia para la reacción
CaCO3 (s) ------- CaO (s)+ CO2 (g)
Es 178.1 KJ/mol.  A partir de los valores de los calores estándar de formación dados en la tabla. Calcule el calor estándar de formación de CaCO3 (s)
Solución:
El cambio estándar de la entalpia en la reacción es
ΔHo = [∆HFO(CaCO)+ ∆HFO (CO2)] - ∆HFOCaCO3)
Substituyendo los valores conocidos, tenemos:
178.1kJ/mol = -635.5 kJ – 393.5 kJ - ∆HFO(CaCO3)
Al resolver para  ∆HFO (CaCO3) tenemos
∆HFO  (CaCO3) = -1207.1 kJ/mol



Autores: 
Paredes Crisanto Daniela y 
Portillo Arreguin Diego Horacio 

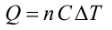
Comentarios

Publicar un comentario

Entradas más populares de este blog

1.1.9. Reacciones exergónicas y endergónicas.

Imagen
Para determinar si una reacción es exergonica o endergonica se necesita saber la diferencia de energía libre  D G.  Cuando la  D G es negativo se dice que dichas reacciones son reacciones exergonicas  porque las moléculas de los reactivos tienen mayor energía que las moléculas de los productos, por lo cual la variación de energía es menor que cero. REACTANTES    →     PRODUCTOS   +   ENERGÍA Cuando su D G es positivo no puede transcurrir espontáneamente porque requiere de un aporte de energía libre y a estas se llaman reacciones endergonicas  porque las moléculas de los reactivos tienen menos energía que las moléculas de los productos, por lo cual la variación de energía es mayor que cero. REACTANTES + CALOR →  PRODUCTOS Ejemplos de reacciones exergonicas: H 2(g)    +  Cl 2(g)   →    2HCl (g...
Leer más

1.2.2 Celdas electroquimicas

Imagen
“Celdas Electroquímicas” ¿Qué son las celdas electroquímicas? Una celda electroquímica es un dispositivo experimental por el cual se puede generar electricidad mediante una reacción química (celda Galvánica). O, por el contrario, se produce una reacción química al suministrar una energía eléctrica al sistema (celda Electrolítica). Estos procesos electroquímicos son conocidos como “reacciones electroquímicas” o “reacción redox” donde se produce una transferencia de electrones de una sustancia a otra, son reacciones de oxidación-reducción. ¿Quiénes las crearon? Las celdas electroquímicas fueron desarrolladas a finales del siglo XVIII por los científicos Luigi Galvani y Allesandro Volta por lo que también se las denomina celda galvánica o voltaica en su honor. ¿Quién es Luigi Galvani? Luigi Galvani (Bolonia, Italia, 9 de septiembre de 1737-ibídem, 4 de diciembre de 1798) fue un médico, fisiólogo y físico italiano, sus estudios le permitieron descifrar la naturaleza eléct...
Leer más

1.2 Procesos Electroquímicos

Imagen
Electroquímica :   Es una rama de la química que estudia la transformación entre la energía eléctrica y la energía química. En otras palabras, las reacciones químicas que se dan entre un conductor eléctrico (llamado electrodo) y un conductor iónico (electrolito). En un sentido más amplio, la electroquímica es el estudio de las reacciones químicas que producen efectos eléctricos y de los fenómenos químicos causados por la acción de las corrientes o voltajes. Entonces los procesos electroquímicos son aquellos en donde se produce la transformación entre la energía eléctrica y la energía química. El campo de la electroquímica ha sido dividido en dos grandes secciones. La primera de ellas es la Electrólisis, la cual se refiere a las reacciones químicas que se producen por acción de una corriente eléctrica. La otra sección se refiere a aquellas reacciones químicas que generan una corriente eléctrica, éste proceso se lleva a cabo en una celda o pila galvánica. ...
Leer más

1.1.1 Sistemas, estados y funciones de estados

Imagen
Cuando estudiamos el intercambio de energía en los procesos que ocurren en la naturaleza, necesitamos definir conceptos como el de  sistema . En las reacciones químicas, el sistema se encuentra formado por las sustancias químicas que intervienen en ellas y el entorno sería todo lo demás. Definición de función de estado. Se debe saber que algunas variables termodinámicas son, además, lo que se conoce como  funciones de estado . ¿Qué significa esto? Significa que si el sistema sufre una modificación y pasa de un estado A a un estado B, el valor de estas variables termodinámicas que son funciones de estado no depende de cómo se ha efectuado la transformación, sólo del estado del sistema. Veremos esto con un ejemplo concreto para que sea más sencillo, tomando como variable la temperatura. Consideremos un sistema que está en un estado A en el cual la temperatura es de 20ºC. Este sistema sufre una transformación y pasa a estar en un estado B en el cual la temperat...
Leer más

1.2.1 Reacciones de Oxidación y Reducción.

Imagen
Reacciones de oxidación y reducción.  Se considera como reacción de transferencia de electrones La oxidación y reducción, también conocida como redox , es un proceso químico en el cual cambia en número de oxidación de un elemento. El proceso puede incluir la transferencia completa de electrones para formar uniones iónicas o sólo una transferencia parcial o desplazamiento de electrones para formar uniones covalentes.  Se efectúa una oxidación cuando aumenta el número de oxidación como resultado de la pérdida de electrones. Y una reducción siempre que el número de oxidación disminuya como resultado    de una ganancia de electrones. La oxidación y la reducción se efectúan simultáneamente en una reacción química; una no puede sucede sin la otra. Oxidación: Incremento del número de oxidación                    Perdida de electrones. Reducción:...
Leer más

1.1.7 Entropía

Imagen
1.1.7 ENTROPÍA   El término entropía se puede utilizar en Física, Química, Psicología, de forma filosófica, en las Empresas, etc. Lógicamente la entropía que nosotros estudiaremos es aquella relacionada con la física y la química. ¿Qué es la Entropía? La entropía es una propiedad de estado en la que importa solamente el estado inicial y final, independientemente de camino recorrido para pasar de uno a otro. La entropía no se define en valores absolutos, se miden cambios (incrementos= Δ) entre uno y otro estado entrópico. Pongamos algún ejemplo para que te queda mucho más claro. Primero un sistema reversible y luego un sistema irreversible (no puede volver al estadoinicial). Ejemplos de Entropía Tenemos una habitación ordenada = Sistema Inicial. Ahora la desordenamos, tiramos la ropa, muebles, etc. Hemos cambiado el sistema inicial y ahora tengo un sistema final = habitación desordenada. Si quieres colocar las cosas para que esté la habitación ...
Leer más

1.1.4 Reacciones exotérmicas y endotérmicas

Imagen
Reacciones  Exotermicas El prefijo  exo  significa “hacia fuera”. Por lo tanto entendemos que las  reacciones exotérmicas  son aquellas que liberan energía en forma de calor. El esquema general de una reacción exotérmica puede ser escrito de la manera siguiente, donde A, B, C y D representan sustancias genéricas. En otras palabras, toda la energía que entró en el primer miembro de la ecuación química, debe salir íntegramente en el segundo miembro de la ecuación. De donde obtenemos la siguiente conclusión:  si una reacción es exotérmica, entonces la entalpía de los reactivos  ( Hr  )  es mayor que la entalpía de los productos ( Hp  ) , pues una parte de la energía que estaba contenida en los reactivos fue liberada para el medio ambiente en forma de calor y apenas otra parte de esa energía quedó contenida en los productos.  Entonces en una reacción exotérmica:  Hr > Hp No es posible determinar directamente la en...
Leer más

1.1.5 Entalpías de enlace.

Imagen
Entalpías de enlace.  También conocida como entalpía de disociación de enlace, energía de enlace promedio o fuerza de enlace. Es la energía almacenada en un enlace entre átomos de una molécula. Específicamente, es la energía que debe agregarse para conseguir la escisión del enlace homolítica o simétrica en fase gaseosa. Un evento homolítico o evento de ruptura de enlace simétrica significa que cuando el enlace se ha roto, cada uno de los átomos que eran parte el enlace original recibe un electrón, convirtiéndose en un radical, en vez de que se forme un ion. La energía de enlace  Es la energía necesaria para romper un mol de enlaces en estado gaseoso. La energía del enlace H-H es mayor que la del enlace Cl-Cl. Esto quiere decir que el enlace en la molécula H 2 , es más fuerte que en la de Cl 2. Las energías de enlace           son siempre positivas, ya que para romper un enlace se requiere energía. El concepto de...
Leer más

1.1.6 Termoquímica. Ley de Hess.

 Termoquímica. Ley de Hess. La   Termoquímica  estudia los cambios energéticos ocurridos durante las reacciones químicas. El calor que se transfiere durante una reacción química depende de la trayectoria seguida puesto que el calor no es una función de estado. Sin embargo, generalmente las reacciones químicas se realizan a P=cte o a V=cte, lo que simplifica su estudio. La situación más frecuente es la de las reacciones químicas realizadas a P=cte, y en ellas el calor transferido es el cambio de entalpía que acompaña a la reacción y se denomina "entalpía de reacción". La entalpía es una función de estado, luego su variación no depende de la trayectoria. La combustión (ver figuras 8.23 y 8.24) es un ejemplo de reacciones químicas donde se liberan grandes cantidades de energía. Por ejemplo, la combustión del hidrógeno que se indica a continuación:    En este caso, el sistema es el hidrógeno, el oxígeno y e...
Leer más